| Numéro |
Nat. Sci. Soc.
Volume 29, Numéro 3, Juillet/Septembre 2021
|
|
|---|---|---|
| Page(s) | 312 - 325 | |
| DOI | https://doi.org/10.1051/nss/2021057 | |
| Publié en ligne | 10 décembre 2021 | |
La croissance verte est-elle durable et compatible avec l’économie circulaire ? Une approche par l’identité IPAT
Is green growth compatible with circular economy? An answer through the IPAT identity
Sciences économiques, Université Savoie-Mont-Blanc, IREGE,
Annecy-le-Vieux, France
* Auteur correspondant : florian.fizaine@gmail.com
Reçu :
28
Novembre
2018
Accepté :
8
Août
2021
Il existe une forte polysémie derrière l’expression « économie circulaire ». Certains identifient l’économie circulaire comme une forme finale de la croissance verte (croissance économique infinie dans un monde fini). D’autres, au contraire, perçoivent la croissance verte comme le prolongement d’un ancien modèle fondamentalement incompatible avec les limites de la géosphère et donc très différent de l’économie circulaire qui s’inscrit dans un mimétisme écologique. Dans cet article, nous explorons les hypothèses permettant de réconcilier la croissance verte avec l’économie circulaire via la dématérialisation. Nous montrons que la réconciliation de l’économie circulaire et de la croissance verte réclamerait (i) une vitesse de décroissance de l’intensité matérielle de l’économie à des niveaux jamais observés, mais également (ii) une absence de limite physique à cette décroissance. Cela laisse supposer que l’approche de la croissance verte est fondamentalement incompatible avec le concept d’économie circulaire.
Abstract
The circular economy concept is currently being used in multiple ways. For some academics and organizations circular economy can be identified as a long term goal of achieved green growth while others argue that circular economy is fundamentally different from green growth. In this paper, we explore the conditions allowing green growth to be compatible with the concept of circular economy. Our model explicitly takes into account the possibility of a dematerializing of wealth production and raw material recycling through a green growth framework. We show that the reconciling of green growth with circular economy requires: (i) a fast decrease of the raw material intensity of economy far removed from present and past trajectories, (ii) the absence of a physical limitation to this decrease. This seems to indicate that green growth is essentially different from, and incompatible with the concept of circular economy.
Mots clés : ressources naturelles / développement durable / découplage / croissance verte / économie circulaire
Key words: natural resources / sustainable development / decoupling / green growth / circular economy
© F. Fizaine, Hosted by EDP Sciences, 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License CC-BY (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, except for commercial purposes, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License CC-BY (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, except for commercial purposes, provided the original work is properly cited.
L’économie circulaire fait couler beaucoup d’encre, notamment quand il s’agit de juger de sa capacité ou non à assurer un réel découplage entre la perpétuation de la croissance économique et la réduction des dégradations faites à l’environnement. Pour éclairer ce débat, l’originalité de la présente analyse économique est de développer un modèle à partir de l’équation IPAT proposée par le biologiste Paul Ehrlich et le physicien John Holdren au début des années 1970 pour mesurer l’impact environnemental de la population humaine. Au terme de son raisonnement, les conditions drastiques auxquelles arrive l’auteur pour qu’une croissance verte puisse s’appuyer sur une économie circulaire apparaissent très éloignées des phénomènes de découplage matériel et énergétique relatif que l’on a pu constater depuis la fin des « Trente Glorieuses ».
La Rédaction
L’économie circulaire est à la mode. Le concept a progressivement remplacé celui de développement durable, probablement du fait du manque d’applicabilité directe de la définition du rapport Brundtland (Kirchherr et al., 2017). Comme son prédécesseur, l’économie circulaire est un concept polysémique intégrant de multiples déclinaisons pratiques sur le terrain : écologie industrielle, production propre, économie de la fonctionnalité, économie du partage (Ghisellini et al., 2016). La plupart des solutions empiriques ont en ligne de mire le découplage entre l’économie et la géosphère (que ce soit en termes d’extraction d’énergie, de matières premières non énergétiques ou d’émissions polluantes).
Le concept d’économie circulaire n’a pas de définition stabilisée mais nous pouvons explorer celle du ministère français de la Transition écologique (MTE) et celle de la fondation Ellen MacArthur. D’après le MTE (2019), le concept d’économie circulaire « désigne un modèle économique dont l’objectif est de produire des biens et des services de manière durable, en limitant la consommation et les gaspillages de ressources (matières premières, eau, énergie) ainsi que la production des déchets. Il s’agit de rompre avec le modèle de l’économie linéaire (extraire, fabriquer, consommer, jeter) pour un modèle économique “circulaire” ». Le concept fut intégré dans la loi de transition énergétique pour la croissance verte du 18 août 2015. Une feuille de route fut ensuite publiée le 23 avril 2018 avec l’ambition « de porter notre modèle d’économie 100 % circulaire au niveau européen et international via l’initiative Make our planet great again ». Cette circularité parfaite se retrouve également chez la fondation Ellen MacArthur (2019) qui identifie Stahel comme l’un des initiateurs du concept d’économie circulaire en 1976 lorsqu’il évoque « les principes d’une économie fonctionnant en circuit fermé (ou économie circulaire) et de son impact sur la création d’emploi, la croissance, la prévention des déchets et la consommation de ressources ».
Bien que le terme soit maintenant largement diffusé, le cadre théorique dans lequel il est mobilisé relance le débat entre partisans d’une croissance dite « verte » et ceux convaincus des limites de la géosphère. En réalité, la question est ancienne et fut âprement débattue au cours des deux derniers siècles. De nombreuses typologies dichotomiques ont émergé pour résumer ces positions irréconciliables : le paradigme du stock fixe contre le paradigme du coût d’opportunité (Tilton, 1996), celui opposant optimistes et pessimistes (Neumayer, 2000), l’économie de l’environnement contre l’économie écologique (Vivien, 1994), la substituabilité forte contre la substituabilité faible1 (Ayres, 2001 ; 2007 ; Rotillon, 2010). Toutefois, il n’existe pas à ce jour de consensus permettant de répondre à la question : le concept de limites à la croissance, sur le long terme, est-il plus pertinent que celui de croissance des limites2 ?
Dans ce cadre, l’émergence de l’économie circulaire et son appropriation par les deux camps sont dénoncées. Certains y voient une solution apte à découpler l’activité économique et la sollicitation de la géosphère, réconciliant ainsi prospérité économique et limites écologiques (McDonough et Braungart, 2011 ; Ellen MacArthur Foundation, 2019 ; Weizsäcker et al., 2013). D’autres estiment que l’économie circulaire ne peut pas être perçue comme un moyen de perpétuer la croissance dans un monde fini et qu’elle ne peut s’envisager que dans un contexte d’état stationnaire, voire de décroissance (Jackson, 2010 ; Grandjean, 2011 ; Arnsperger et Bourg, 2016 ; Ghisellini et al., 2016 ; Kirchherr et al., 2017). Les débats ne sont pas seulement idéologiques car de ces deux positions naissent des remèdes différents. Dans le premier cas, les contradictions écologiques pourraient être dépassées par l’internalisation des externalités et un juste système de prix, les mécanismes de marché et le changement technique faisant le reste. Au contraire, dans le second cas, l’arithmétique de l’écologie et celle de la croissance économique illimitée ne sont pas compatibles, et une refondation de nos sociétés sur des principes alternatifs à ceux de la croissance de la production (même verte) est nécessaire.
Dans cet article, nous cherchons à étudier les conditions de réconciliation entre l’économie verte et l’économie circulaire. Pour ce faire, nous étudions les paramètres permettant d’avoir une croissance verte de l’activité économique ne s’appuyant pas sur un prélèvement croissant de ressources naturelles. Pour devenir durable sur le long terme, la croissance verte doit pouvoir s’appuyer sur un stock constant de ressources naturelles compte tenu des capacités finies de la planète. Le stade ultime de l’économie circulaire visant l’indépendance vis-à-vis de la géosphère en termes de prélèvement net en ressources (extraction de ressources primaires non renouvelables). Pour réduire ce prélèvement (sur des ressources renouvelables ou non), l’United Nations Environment Program (UNEP) a opté pour une stratégie s’appuyant sur le découplage via la substitution et l’efficacité/productivité en ressources3 (UNEP, 2011 ; 2016). Bien que l’économie expérimente un découplage relatif (les prélèvements en ressources progressent moins vite que le PIB), il s’agit à terme d’atteindre un découplage absolu, c’est-à-dire une diminution ou une stagnation des prélèvements en ressources primaires tandis que le PIB augmente (Jackson, 2010).
Cet article contribue à la littérature en examinant explicitement le lien entre la croissance économique et la consommation de ressources naturelles. D’autres articles plus anciens ont déjà souligné les limites du recyclage dans le cadre d’une croissance de la consommation de ressources naturelles (Radetzki et Van Duyne, 1985 ; Grosse et Mainguy, 2010 ; 2011 ; Labbé, 2016). Toutefois, ces recherches ne font pas de liaison explicite avec l’augmentation de la taille de l’économie alimentant pourtant la croissance matérielle de la consommation, mais partent du présupposé de l’augmentation de cette dernière. Or, les avocats de la croissance verte défendent la possibilité d’un découplage entre croissance de l’économie et croissance matérielle via la hausse de l’efficacité matérielle, équivalente à une baisse de l’intensité matérielle de la richesse (Laurent, 2011). Nous introduisons donc également la possibilité d’une baisse de l’intensité matérielle de la richesse. Nos conclusions partagent un grand nombre de points communs avec les positions de Fagnart et Germain (2011 ; 2012), en particulier sur les contraintes reliées à la productivité des ressources naturelles. Toutefois, le modèle de croissance employé par ces auteurs nécessite des hypothèses particulières, notamment sur la forme de la fonction de production. En outre, leur modèle postule encore un recyclage parfait de la ressource naturelle essentielle utilisée dans l’économie. Finalement, le haut degré de complexité et d’abstraction du modèle conduit à une simulation numérique non calibrée sur différentes formes de données empiriques réelles. C’est pourquoi nous pensons qu’un modèle accessible basé sur l’identité comptable « Impact Population Affluence Technology » (IPAT), dont on observe facilement et explicitement l’évolution réelle des termes, est susceptible de compléter l’approche adoptée par ces auteurs.
Le modèle
Représentation comptable de la consommation de ressources naturelles
Notre modèle s’inspire de l’identité comptable IPAT formulée par Ehrlich et Holdren (1971). Cette identité est très populaire dans le domaine des analyses de l’économie écologique, que ce soit dans des études économétriques ou au travers des analyses de flux de matières (Steinberger et al., 2010). Elle a aussi le mérite de permettre de dissocier les questions de croissance démographique et de croissance économique du revenu par habitant. L’identité IPAT retranscrit l’impact environnemental en termes de consommation de ressources ou de pollution (I) comme le produit de trois facteurs : la population (P), le revenu par habitant (A) et le changement technologique (T). Ce dernier facteur (T) est traditionnellement perçu au travers de l’intensité matérielle de l’économie (IM)4. Celle-ci est calculée comme le ratio de la consommation en ressources sur le PIB et exprime le contenu moyen en ressources naturelles d’une unité de richesse créée. On peut donc exprimer la consommation initiale en ressources de l’économie (Ct = 0) comme :
 (1)
(1)
Passage à une vision dynamique
En introduisant de la dynamique, nous pouvons obtenir la trajectoire de l’économie en termes de consommation de ressources à l’année t :
 (2)
(2)
La consommation de ressources naturelles durant l’année t dépend du niveau initial de consommation et du taux de croissance annuel de nos trois facteurs : 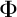 représente le taux de croissance de la population,
représente le taux de croissance de la population, 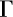 le taux de croissance du revenu par habitant, Z le taux de croissance de l’intensité en ressources naturelles d’une unité de richesse et t l’année étudiée. Un Z négatif peut résulter du changement technique (efficacité matérielle/productivité de la ressource) à un niveau aggloméré ou d’un effet de substitution entre deux ressources naturelles à un niveau désagrégé (transmatérialisation). On suppose ici que les taux de croissance des différents paramètres sont constants, ce qui n’est pas nécessairement représentatif de la réalité.
le taux de croissance du revenu par habitant, Z le taux de croissance de l’intensité en ressources naturelles d’une unité de richesse et t l’année étudiée. Un Z négatif peut résulter du changement technique (efficacité matérielle/productivité de la ressource) à un niveau aggloméré ou d’un effet de substitution entre deux ressources naturelles à un niveau désagrégé (transmatérialisation). On suppose ici que les taux de croissance des différents paramètres sont constants, ce qui n’est pas nécessairement représentatif de la réalité.
Introduction d’une possibilité de croissance verte par découplage absolu
Un grand nombre d’études ont montré qu’un prélèvement annuel croissant de ressources naturelles à partir de la géosphère n’est pas tenable à long terme (Meadows et al., 1972 ; Rockström et al., 2009). Remarquons qu’une façon de diminuer la consommation annuelle de ressources naturelles tout en maintenant la croissance verte consiste à faire descendre à un rythme plus rapide l’intensité en ressource d’une unité de richesse relativement à la croissance du revenu par habitant (à population égale). Précisément, la consommation annuelle en ressources primaires peut baisser dans un contexte de croissance verte (on parle alors de découplage absolu) si :
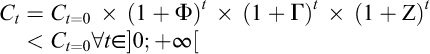 (3)
(3)
Soit en simplifiant et en exprimant en fonction de Z, on obtient le niveau Z* de découplage absolu :
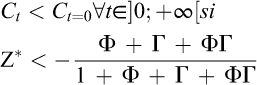 (4)
(4)
Quand la croissance de la population est nulle ( ), on obtient alors :
), on obtient alors :
 (5)
(5)
Conclusion 1 : La consommation matérielle de l’économie peut décroître dans une économie en croissance (Γ > 0) si Z, c’est-à-dire le taux de variation de l’intensité matérielle, est suffisamment négatif.
Toutefois, l’économie consomme des ressources naturelles dont les conditions de soutenabilité sur le long terme sont très différentes. C’est pourquoi nous distinguerons les résultats selon que la ressource étudiée est (a) un stock non renouvelable et non recyclable (énergie fossile), (b) un flux renouvelable non recyclable (énergie solaire et éolienne), (c) un stock non renouvelable et recyclable (ressources minérales et métaux), (d) un stock renouvelable et recyclable (biomasse).
Stock de ressources non renouvelables et non recyclables
Maintenant définissons le rythme général de la consommation de ressources naturelles en cas de découplage absolu comme :
 (6)
(6)
Où  peut être perçu comme le taux de croissance du niveau de prélèvement en ressources naturelles. Une baisse de la consommation pouvant avoir lieu dès lors que
peut être perçu comme le taux de croissance du niveau de prélèvement en ressources naturelles. Une baisse de la consommation pouvant avoir lieu dès lors que 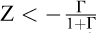 (découplage absolu). Dans ces conditions et en intégrant un stock fini de ressources, est-il possible de suivre indéfiniment un rythme de croissance verte ? Plus formellement, nous cherchons à déterminer si la consommation cumulée de ressources de l’économie (S) est strictement inférieure à l’infini quand T tend vers l’infini :
(découplage absolu). Dans ces conditions et en intégrant un stock fini de ressources, est-il possible de suivre indéfiniment un rythme de croissance verte ? Plus formellement, nous cherchons à déterminer si la consommation cumulée de ressources de l’économie (S) est strictement inférieure à l’infini quand T tend vers l’infini :
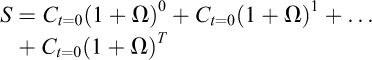 (7)
(7)
Or, lorsque T tend vers l’infini et  , cette suite tend vers :
, cette suite tend vers :
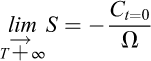 (9)
(9)
Dans ces conditions, la consommation cumulée va tendre vers une limite finie positive de ressources naturelles. Reste à déterminer si cette limite est supérieure ou non au stock total de ressources naturelles.
Conclusion 2 : Si, du fait d’un découplage suffisamment rapide (découplage absolu), la consommation de ressources naturelles décroît continuellement à un rythme géométrique, il est possible de croître économiquement sans limite en s’appuyant sur un stock fini de ressources. Cette conclusion possède comme corollaire qu’un prélèvement croissant ou même constant en ressources (Ω ≥ 0), du fait d’une intensité matérielle qui ne parvient plus à baisser suffisamment rapidement (Z > Z*), rend impossible la croissance économique sans limite sur un stock fini de ressources. Cette hypothèse repose sur l’intuition que l’intensité matérielle et l’intensité énergétique ne pourront pas descendre asymptotiquement à zéro compte tenu du fait que même les services reposent sur un substrat matériel et énergétique strictement positif5.
Flux de ressources renouvelables et non recyclables
Notons que, dans le cas d’un flux de ressource renouvelable non recyclable (comme l’énergie éolienne ou solaire), le problème ne se pose pas dans les mêmes termes. Dans ce cas, l’économie ne peut pas consommer davantage qu’un flux annuel positif maximum (β) :
 (10)
(10)
On peut alors déterminer la durée maximale de cette croissance verte (T*) en fonction des autres paramètres :
 (11)
(11)
L’étude de cette équation montre que T* tend vers l’infini lorsque Z se rapproche du niveau de découplage absolu (Z*). En cas de découplage absolu, c’est-à-dire dans une situation où l’intensité en ressources baisserait plus vite que la taille de l’économie n’augmenterait, le prélèvement annuel β maximum ne serait jamais atteint et l’économie pourrait croître indéfiniment. Au contraire, si on suppose à nouveau que l’intensité en ressources (par exemple, le contenu énergétique d’une unité de richesse) ne pourra pas descendre asymptotiquement jusqu’à zéro, et donc que Z ne pourra pas être éternellement suffisamment négatif, T* est alors fini. La figure 1 montre l’évolution de la durée maximale de croissance économique du revenu selon la vitesse de dématérialisation Z de l’économie, avec des valeurs paramétrées sur l’énergie solaire annuelle absorbée par la Terre (une ressource renouvelable non recyclable) et la consommation actuelle d’énergie finale.
Conclusion 3 : S’il existe une limite physique positive au contenu en ressource d’une unité de richesse, alors il n’est pas possible de croître de façon illimitée sur un flux annuel constant non recyclable de ressources. Au contraire, si Z est suffisamment important pour que l’économie connaisse une situation de découplage absolu et qu’il n’existe pas de limite plancher à l’intensité en ressource, on peut croître indéfiniment.
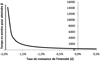 |
Fig. 1 Durée pour atteindre un seuil β en fonction de l’évolution de l’intensité Z. Les valeurs des paramètres Φ, Γ, C0 et β ont été fixées à 0 % ; 2 % ; 13,541 Gtep ; 91,955 Gtep. Note : Gtep signifie milliards de tonnes d’équivalent pétrole. β correspond au flux d’énergie solaire absorbé par la terre par an et C0 représente la consommation d’énergie finale actuelle humaine. |
Ressources de stocks non renouvelables et recyclables : cas de l’économie circulaire
Dans le cas d’une ressource non renouvelable mais recyclable, la question d’une économie parfaitement circulaire se pose, c’est-à-dire la possibilité que nos déchets deviennent nos ressources. Nous introduisons donc la possibilité d’un recyclage à l’issue de la durée de vie des biens (c’est-à-dire le temps de passage de la ressource naturelle dans l’économie). Notre équation de consommation nette (CN) de ressources primaires, c’est-à-dire la consommation totale déduite du recyclage, devient alors :
 (12)
(12)
Où i représente le temps de passage générique de la matière dans l’économie et α le taux de recyclage de la matière à l’issue de son passage dans l’économie6. Cette équation peut aussi être reformulée par :
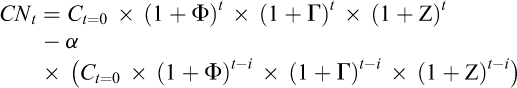 (13)
(13)
Pour avoir un bouclage complet du bilan matière et ne plus avoir à extraire des ressources naturelles de la géosphère pour alimenter l’économie, il faut nécessairement que le recyclage corresponde à la demande en ressources de l’économie. En résolvant l’équation (13) avec CNt = 0 et en simplifiant, nous obtenons :
 (14)
(14)
Bien entendu, il existe des conditions triviales qui garantissent l’économie circulaire, à savoir un taux de recyclage parfait ( ) associé à une durée de vie nulle (recyclage immédiat des produits). Nous excluons cette possibilité compte tenu des contraintes physiques du monde réel.
) associé à une durée de vie nulle (recyclage immédiat des produits). Nous excluons cette possibilité compte tenu des contraintes physiques du monde réel.
Étudions maintenant les conditions dans lesquelles le système économique peut croître indéfiniment dans le cadre de l’économie circulaire. Pour cela, nous exprimons l’équation (14) en fonction de la baisse d’intensité matérielle Z et nous obtenons alors le niveau qui permet la circularité :
 (15)
(15)
En reprenant l’équation (15), nous pouvons définir le niveau de découplage nécessaire pour assurer la croissance verte en boucle fermée. Nous utilisons les valeurs des paramètres suivantes pour la population et la croissance du PIB/habitant :  et
et  . Ces fonctions sont représentées sur la figure 2 pour différents temps de passage de la matière dans l’économie (i).
. Ces fonctions sont représentées sur la figure 2 pour différents temps de passage de la matière dans l’économie (i).
Pour atteindre un état d’économie circulaire, il existe une condition nécessaire mais non suffisante : 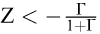 . Autrement dit, il faut que l’intensité matérielle d’une unité de richesse décroisse suffisamment vite par rapport au taux de croissance du revenu par habitant (découplage absolu : droite zébrée sur la figure 2). Par exemple, avec un taux de croissance de l’économie de 3 % par an, il faut que l’intensité matérielle baisse au moins de 2,91 % par an. Toutes les solutions nécessitent a minima cette variation à la baisse de l’intensité matérielle (courbes inférieures à la ligne de découplage sur la figure 2). Bien entendu, plus le taux de croissance économique par tête (et démographique) visé sera important, plus il sera difficile d’atteindre l’objectif d’une économie circulaire.
. Autrement dit, il faut que l’intensité matérielle d’une unité de richesse décroisse suffisamment vite par rapport au taux de croissance du revenu par habitant (découplage absolu : droite zébrée sur la figure 2). Par exemple, avec un taux de croissance de l’économie de 3 % par an, il faut que l’intensité matérielle baisse au moins de 2,91 % par an. Toutes les solutions nécessitent a minima cette variation à la baisse de l’intensité matérielle (courbes inférieures à la ligne de découplage sur la figure 2). Bien entendu, plus le taux de croissance économique par tête (et démographique) visé sera important, plus il sera difficile d’atteindre l’objectif d’une économie circulaire.
Conclusion 4 : pour boucler, c’est-à-dire ne consommer aucune nouvelle unité de ressource naturelle primaire, l’intensité matérielle dans un contexte de croissance économique doit être égale ou inférieure à : 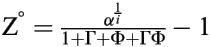 . 7
. 7
Comme on peut le voir sur la figure 2, l’atteinte de l’économie circulaire est d’autant plus aisée que le taux de recyclage est élevé et/ou la durée de vie des produits longue. L’un des résultats importants mis en avant par cette étude repose sur la possibilité d’une économie circulaire avec bouclage complet de la matière sans recyclage complet (impossible d’un point de vue physique). Il « suffit » pour cela d’avoir une durée de vie des produits suffisamment élevée et un taux de décroissance de l’intensité matérielle suffisamment rapide par rapport au taux de croissance du revenu par tête. Toutefois, à nouveau, si l’on suppose que l’intensité matérielle ne peut pas baisser en dessous d’un niveau « plancher » fixé à une grandeur positive quelconque a, on peut démontrer que l’économie circulaire ne pourra être atteinte que pendant une durée limitée en présence de croissance. En effet, supposons que l’intensité matérielle IMt soit réduite chaque année du niveau de dématérialisation Z° fixé par l’équation (15) :
 (16)
(16)
Où VI est la valeur initiale de l’intensité matérielle (contenu matériel par unité de richesse créée). Si on introduit une limite physique a stipulant qu’il faut toujours une base matérielle et énergétique minimale à la création d’une unité de richesse et que l’on exprime en fonction de t, nous obtenons t° :
 (17)
(17)
Autrement dit, la durée pendant laquelle nous pouvons atteindre l’économie circulaire grâce à un niveau de dématérialisation fixé par l’équation (15) est d’autant plus longue que la différence entre la valeur initiale d’intensité matérielle et le seuil plancher est importante mais également que la vitesse de dématérialisation est faible. On remarquera que l’étude des limites de l’équation (17) avec (VI > a > 0) et (Z < 0) implique que si a tend vers 0 :
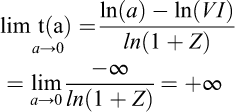 (18)
(18)
La durée possible de dématérialisation (t) peut tendre vers l’infini si a (la limite physique) tend vers 0.
Conclusion 5 : En présence d’une limite positive physique minimale à l’intensité matérielle de l’économie, l’atteinte de l’économie circulaire par la dématérialisation ne peut être que temporaire et d’une durée t finie.
Par conséquent, l’économie circulaire perpétuelle en présence de croissance verte requiert une double condition : la première implique que les niveaux des paramètres Z, α et i soient suffisants relativement à la croissance du revenu ( ). Cela nécessite, entre autres, un Z suffisamment négatif (inférieur au seuil de découplage absolu). La seconde est qu’il ne doit pas exister une limite physique plancher à la dématérialisation de la richesse.
). Cela nécessite, entre autres, un Z suffisamment négatif (inférieur au seuil de découplage absolu). La seconde est qu’il ne doit pas exister une limite physique plancher à la dématérialisation de la richesse.
 |
Fig. 2 Niveau de baisse de l’intensité matérielle nécessaire (découplage) pour concilier croissance verte illimitée et économie circulaire. Les courbes représentent le niveau nécessaire de recyclage et de variation de l’intensité matérielle pour différentes valeurs de durée de vie des produits en années. Note : Φ = 0 et Γ = 0,03. |
Ressources de stock renouvelables et recyclables
Enfin, dans le cas d’une ressource de stock comme la biomasse qui serait à la fois renouvelable et recyclable, il serait possible d’avoir une consommation nette du recyclage strictement positive car la biosphère est capable (sous condition d’un stock naturel suffisant et peu dégradé8) de fournir un flux annuel constant δ. Ce flux annuel constant est supposé fini. Le problème consiste alors à trouver les solutions en fonction de Z permettant d’égaliser l’équation (13) avec le flux constant δ fourni par la nature. Il n’existe alors plus de solutions analytiques générales9, mais l’on peut trouver des solutions numériques et dynamiques de Z pour des valeurs particulières des paramètres.
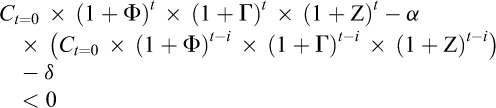 (19)
(19)
L’équation (19) peut être réexprimée en fonction de λ, un paramètre représentant le multiple entre le prélèvement maximum possible et la taille de l’économie initiale ( ) :
) :
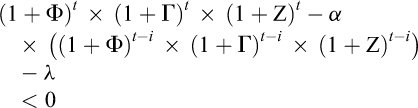 (20)
(20)
Comme nous pouvons l’observer avec des simulations utilisant des valeurs empiriques des paramètres du papier/carton (Krausmann et al., 2017), la vitesse de dématérialisation dépend ici de t (Fig. 3). Le respect de l’équation (20) nécessite d’avoir un Z inférieur aux courbes en pointillé (selon le multiple λ retenu). Globalement, les conditions nécessaires relatives à la vitesse de dématérialisation sont moins exigeantes que pour une ressource recyclable et non renouvelable (δ = 0), en particulier sur le long terme.
Conclusion 6 : Sur le court terme, si on autorise un prélèvement annuel positif sur la biosphère, assurer une croissance verte grâce au processus de dématérialisation (Z) dépend essentiellement de la taille du prélèvement par rapport à la consommation initiale (λ), du taux de recyclage (α) et de la durée de vie de la matière dans l’économie (i). Sur le long terme, le niveau de découplage requis pour continuer à croître indéfiniment implique d’assurer une vitesse de dématérialisation a minima égale au découplage absolu (Z*).
Nous allons maintenant analyser empiriquement si l’atteinte de cette économie circulaire par la croissance verte est un objectif plausible ou pas.
 |
Fig. 3 Vitesse de dématérialisation requise (Z) à différentes dates appliquée au cas du carton/papier. Note : λ représente le ratio entre le prélèvement maximum autorisé sur la biosphère en ressources et la consommation en ressources de l’économie initiale. Note : Φ = 0, Γ = 2 %, i = 2, α = 34 %. Dans le cas de λ = 0 (consommation primaire nulle), il faudrait que Z soit inférieur à −42 % par an. |
Application
Pour déterminer la position de l’économie mondiale, nous explorons le niveau nécessaire de découplage pour des valeurs réelles des paramètres (Φ, Γ, α, i). Les valeurs empiriques sont précisées dans le tableau 1. Comme nous pouvons l’observer sur la figure 4, la croissance du PIB et les consommations de diverses ressources sont étroitement corrélées. Les mesures du taux de croissance de la population et du PIB mondial (en dollar international constant 1990) sont tirées de l’ONU, de Maddison (2007) et du Maddison Project (2013). Nous proposons l’estimation des paramètres sur le recyclage, la durée de vie et la croissance de la consommation totale pour 11 types de ressources sur la période 1950-2010 à partir des données offertes par Krausmann et al. (2017). Nous proposons également une mesure agrégée représentant la moyenne pondérée (par le poids en base 2010) des 11 ressources de l’étude précédente (Tab. 1) ainsi que des mesures alternatives (Tab. 2) appuyées sur les données de Krausmann et al. (2009) et celles de Fizaine et Court (2016).
Sur la période 1950-2010, l’économie mondiale a connu une croissance annuelle moyenne de 3,94 % tirée davantage par l’évolution du niveau de vie (+2,23 %) que par la croissance démographique (+1,68 %). L’observation du tableau 1 montre que la situation peut être assez contrastée selon les ressources, passant d’un découplage relatif pour le bois (Z = −2,62 %/an) à une forte hausse du contenu en plastique du PIB (Z = 5,05 %/an). Au niveau agrégé, l’intensité n’a pas évolué (0,01 %/an). Cette mesure est toutefois discutable et d’autres indicateurs d’intensité matérielle et énergétique montrent des niveaux de découplage relatif variables selon les périodes (Tab. 2). Cependant, dans le meilleur des cas, l’augmentation de la productivité des ressources est loin d’être suffisante pour atteindre un niveau de découplage absolu (et non pas seulement relatif). Cela s’observe notamment au travers de la croissance de la consommation moyenne par an de toutes les ressources (Ω) sur cette période. Le niveau requis de dématérialisation pour atteindre un découplage absolu sur cette période afin de permettre une stagnation de la consommation de ressources aurait nécessité une baisse de l’intensité de −3,80 % par an, bien loin du +0,01 % constaté en moyenne (Tab. 1). Selon les ressources, le rythme nécessaire pour obtenir une stagnation de la consommation devrait d’ailleurs être d’une fois et demie (bois) à huit fois (papier et acier) plus rapide que ce qui a été observé.
Compte tenu du niveau de recyclage des différentes ressources au niveau mondial, mais aussi de la durée de vie moyenne de leurs usages dans l’économie, l’économie circulaire parfaite semble un objectif encore plus difficilement accessible qui requerrait une baisse de l’intensité matérielle d’environ 6,34 % par an au niveau agrégé (Z° = −6,34 %, Tab. 1). Évidemment, cet objectif très ambitieux pourrait être abaissé si le recyclage et la durée de vie des produits augmentaient en parallèle. Par exemple, en accroissant de 1 % la durée de vie des produits contenant de l’acier, on abaisse de 0,09 % l’objectif de baisse d’intensité nécessaire, tandis qu’une hausse de 1 % du niveau de recyclage de cette ressource réduirait de 0,52 % ce même objectif. Toutefois, même avec des niveaux de recyclage et des cycles de vie ambitieux (95 % et 50 ans respectivement), l’objectif de baisse d’intensité matérielle réclamerait un effort annuel encore particulièrement important (−3,83 % par an), loin des −0,51 % annuels de l’acier.
Plutôt que d’accentuer la vitesse de dématérialisation, une autre possibilité consisterait à ralentir le rythme de croissance de l’économie verte. Cela aurait pour conséquence d’abaisser « la cible » du découplage absolu (Z*) et celle de l’atteinte de l’économie circulaire (Z°). Dans des conditions de croissance de la population nulle et d’une augmentation modérée du revenu par habitant (1 %), l’évolution de l’intensité matérielle à obtenir ne nécessite « plus qu’une » baisse de 0,99 % par an pour stabiliser la consommation (découplage absolu) et de −2,35 % par an pour parvenir à l’économie circulaire (avec i = 50, α = 50 %). Reste à déterminer dans quelle mesure cette baisse de la croissance économique est susceptible d’être compatible avec d’autres objectifs sociaux, financiers et fiscaux.
Rappelons que nous ignorons ici la possibilité d’une limite plancher à la baisse de l’intensité matérielle. En effet, en introduisant cette limite et en réutilisant l’équation (17), nous pouvons comprendre que la réconciliation de l’économie circulaire, même avec des vitesses élevées de dématérialisation telles que suggérées plus haut, ne peut être que temporaire et de plutôt courte durée. Ainsi, comme le montre le tableau 3, même en supposant des possibilités de gains d’efficacité matérielle encore très importants (un facteur 5010), des taux élevés de dématérialisation comme ci-dessus (−6 % par an) ne peuvent se prolonger, au mieux, que sur quelques décennies (63 ans).
Valeurs empiriques des différents paramètres du modèle sur la période 1950-2010. *Ces ressources sont potentiellement renouvelables ou peuvent être produites à partir de ressources renouvelables ; les conditions sur l’économie circulaire peuvent donc être moins restrictives que Z° et se rapprochent de Z* sur le long terme. Source : Krausmann et al. (2017), ONU, Maddison (2007) et Maddison Project (2013).
 |
Fig. 4 Évolution de la consommation d’énergie, de cuivre et de matières premières et du produit intérieur brut mondial (base 100 = 2009). Données : Maddison Project (2013), Krausmann et al. (2017), Fizaine et Court (2016). |
Évolution de l’intensité de différentes mesures agrégées au niveau mondial. Note : intensité matière basée sur les données de Krausmann et al. (2009), intensité énergétique basée sur les données de Fizaine et Court (2016).
Temps estimé pour atteindre un minimum en intensité matérielle selon le rapport entre la valeur initiale (VI) et le seuil minimal (a) ainsi que la vitesse de dématérialisation Z.
Discussion
Nous pouvons tirer deux conclusions majeures de notre modèle et de son application sur les données réelles. D’abord, la réconciliation de la croissance verte illimitée avec l’économie circulaire requiert une vitesse de dématérialisation de la richesse créée bien plus rapide que celle constatée jusque-là. Ensuite, l’existence d’un plancher positif à la baisse de l’intensité matérielle (limite asymptotique positive) condamne la possibilité d’une réconciliation définitive de la croissance verte avec une économie authentiquement circulaire.
Politiques susceptibles d’accélérer la baisse de l’intensité matérielle
Le débat peut donc consister à s’interroger sur les moyens d’accélérer la baisse de l’intensité matérielle de l’économie (efficacité matérielle). Il existe potentiellement deux voies pour ce faire. La première solution peut jouer sur l’effet de structure. Comme certains secteurs sont moins intensifs en ressources naturelles pour générer de la valeur ajoutée, augmenter leur part dans le PIB abaisserait l’intensité matérielle de l’économie. Toutefois, Jackson (2010) estime que cette option pourrait potentiellement freiner la croissance dans la mesure où ces secteurs peu intensifs en ressources naturelles sont aussi des secteurs caractérisés par de plus faibles taux de croissance. Basculer vers ces derniers réduirait donc d’autant les possibilités de croissance verte. Une seconde solution s’appuie sur l’efficacité matérielle, c’est-à-dire sur l’augmentation de la productivité des ressources. D’après Weizsäcker et al. (2013), des gisements potentiellement très importants d’efficacité existent mais ne seraient que partiellement déployés du fait d’un prix très bas de l’énergie et des ressources naturelles.
D’autres pistes envisagent de changer radicalement le modèle commercial des produits via la « servicisation » de l’économie (Stahel, 2014), c’est-à-dire un modèle où l’activité économique serait fondée sur l’achat d’une prestation de service plutôt que sur la possession d’un bien (économie de la fonctionnalité). Il s’agit de fournir des incitations au maintien des appareils en fonctionnement dans l’optique d’allonger le cycle de vie de la matière et de diminuer la demande matérielle associée à ces biens. Pour continuer, l’économie du partage est aussi susceptible de générer d’importants gains de productivité en ressources naturelles. Ainsi, le covoiturage permet d’utiliser plus efficacement une voiture, le prêt d’outils aussi.
Toutefois, si ces solutions peuvent nous permettre d’abaisser considérablement l’intensité matérielle de l’économie, elles ne sont pas reproductibles sans fin. En effet, après l’optimisation de l’usage des voitures (en les employant 95 % du temps et en maximisant leur remplissage, ce qui est déjà compliqué à mettre en œuvre), il ne sera plus possible d’intensifier l’usage de ces dernières pour faire baisser l’intensité matérielle et énergétique du service de déplacement. Par ailleurs, l’existence d’un minimum théorique à la baisse de l’intensité matérielle implique que les gains de productivité devraient devenir de moins en moins importants au fur et à mesure que l’on se rapproche de la limite théorique positive (Z se rapprocherait alors de 0), rebasculant alors l’économie hors de l’économie circulaire. Il semble par conséquent que l’existence de cette limite théorique apparaisse comme critique puisqu’elle exclut ou non la possibilité d’une économie circulaire perpétuelle et donc la possibilité d’une croissance verte. Le rejet de cette limite positive nécessiterait de démontrer l’existence d’une activité économique pouvant réduire progressivement et sans limite son assise matérielle ou, au contraire, augmenter sans plafond sa valeur ajoutée. C’est pourquoi d’autres auteurs militent pour un ralentissement de la croissance (Grosse et Mainguy, 2010), l’état stationnaire (Daly, 1979 ; Arnsperger et Bourg, 2017), voire la décroissance (Georgescu-Roegen, 1971). Diminuer la croissance économique soulève toutefois d’autres dilemmes que nous n’aborderons pas dans le cadre de cet article.
Comparaison avec d’autres solutions communément envisagées
Notre modèle peut aussi répondre à l’intégration d’autres effets. Ainsi, la solution de Daly (1990) entrevoit une économie soutenable à long terme comme une société ne s’appuyant que sur des flux de ressources renouvelables. Cela ne change pas radicalement les conclusions du modèle, la seule différence est que nous admettons que le prélèvement en ressources primaires peut être positif et non nul comme dans le cas des ressources non renouvelables [équation (19) au lieu de (14)]. Bien entendu, ce prélèvement est borné à la hausse, il possède une limite positive qui est non extensive et finie. La capacité de production de biomasse est, en effet, limitée par la surface exploitable et le rendement énergétique théorique maximum de la photosynthèse (Bihouix, 2014). Ici, il réside aussi un problème d’échelle dans cette substitution massive du non-renouvelable par le renouvelable. D’une part, l’usage des ressources non renouvelables par notre économie dépasse de très loin celui des ressources renouvelables (facteur 4) et ce fossé s’accentue avec le temps (Fig. 5). En réalité, la seule véritable dématérialisation d’envergure effectuée par nos économies fut celle engagée dans l’abandon des ressources renouvelables au profit des ressources épuisables (Krausmann et al., 2009). D’autre part, le dépassement actuel de l’empreinte écologique (basée sur des ressources renouvelables) questionne notre capacité à substituer l’ensemble de notre bilan en ressources non renouvelables par des ressources renouvelables11 (Boutaud et Gondran, 2009).
On peut également discuter de la possibilité de jouer sur le paramètre du taux de croissance de la population. Si, par le passé, celui-ci a évolué de façon défavorable, c’est-à-dire contre l’atteinte du découplage et de l’économie circulaire, le plafonnement puis le déclin de la population mondiale suite à la transition démographique pourraient considérablement rapprocher la cible de l’économie circulaire [équation (15)]. Ainsi, selon l’ONU, des pays comme le Japon ou la Bulgarie, en tête dans le phénomène du vieillissement de la population mondiale, atteignent déjà des taux de réduction de la population autour de −0,6 % par an et devraient osciller dans la fourchette −0,6 % à −0,95 % par an d’ici à 2100. Pourtant, là encore, le déclin de la population mondiale pour des raisons naturelles (transition démographique) ou coercitives (politiques malthusiennes) ne va pas sans poser, lui aussi, un certain nombre de problèmes d’équilibre économique (demande globale, disponibilité de l’épargne, système de retraites). Par ailleurs, un déclin plus rapide de la population (Φ suffisamment négatif) relativement à la croissance du revenu par tête conduirait à la décroissance du PIB, ce qui équivaudrait aux solutions avancées plus haut (ralentissement ou disparition de la croissance économique).
 |
Fig. 5 Bilan mondial de l’extraction de ressources naturelles par catégorie. Les ressources renouvelables (biomasse) ne représentent qu’une part minoritaire du bilan et leur poids relatif décroît. Données de l’UNEP (2016). |
Différence entre la problématique de découplage pollution-PIB et ressources/énergie-PIB
Bien entendu, la disponibilité des ressources naturelles pour la croissance n’est pas la seule limite écologique. L’urgence climatique impose de découpler avant tout l’économie des limites exutoires de la planète. Une approche similaire à celle présentée ici serait possible via l’identité de Kaya (Jackson, 2010). Toutefois, le problème ne se pose pas dans les mêmes termes. En effet, il n’existe pas de limite « plancher » à la baisse de l’intensité carbone de l’énergie (on peut/sait produire de l’énergie sans carbone et construire des systèmes énergétiques avec de l’énergie décarbonée). Le découplage carbone-énergie pose un problème de coûts, de gestion politique des défaillances de marché, d’absence de consensus mondial pour gérer l’internalisation d’externalités, mais surtout de dynamique car notre capacité à passer suffisamment vite à des systèmes énergétiques décarbonés est limitée. Toutefois, cela n’exclut pas d’avoir une société sans carbone à très long terme. A contrario, une limite « plancher » du contenu en énergie et en matière de la richesse créée autoriserait seulement un découplage ressources/énergie de l’économie pendant un temps limité : celui de l’atteinte du plancher. Par conséquent, la réconciliation de la croissance verte avec l’économie circulaire ne pourrait être, au mieux, que transitoire.
Conclusion
Dans cet article, nous avons discuté le renouvellement des positions « pro » et « anti » « limites à la croissance ». Le débat est ancien mais il connaît une résurgence via la lutte pour l’appropriation du concept d’économie circulaire. Dans le camp des partisans de la croissance verte (abondancistes), l’économie circulaire est un nouveau relais de croissance à même de résoudre l’inconciliable duo croissance illimitée dans un monde fini. Ces derniers mettent en avant principalement le recyclage et la dématérialisation (alternativement les gains de productivité ou d’efficacité matérielle) pour résoudre cet antagonisme. Au contraire, le camp des pessimistes revendique l’impossibilité de faire croître sans limite l’économie circulaire.
C’est pourquoi nous étudions cette problématique sous l’angle de l’équation IPAT, en intégrant à la fois les possibilités de recyclage et de dématérialisation de l’économie. Nous tirons deux conclusions principales du modèle : (i) le découplage devrait être bien plus rapide pour permettre une croissance verte illimitée. Le niveau requis est bien plus élevé que les niveaux observés jusqu’à aujourd’hui (un facteur 1,5-8 a minima). Le recyclage et l’allongement du cycle de vie de la matière peuvent rapprocher la cible de l’économie circulaire mais sans changer radicalement la chose ; (ii) l’existence d’un plancher à la baisse dans le contenu en matière d’une unité de richesse créée condamne la possibilité d’une croissance verte perpétuelle et rend donc irréconciliables économie circulaire et croissance verte.
Si notre modèle exclut la possibilité d’une croissance verte dans le cadre de l’économie circulaire, rien n’interdit toutefois la circularité dans le cadre d’une économie en état stationnaire, à condition que le substrat matériel sur lequel s’appuie la société soit constitué majoritairement de ressources renouvelables et que le prélèvement (recyclage déduit) soit inférieur au taux de régénération de la ressource renouvelable. Pour l’énergie, le prélèvement maximal annuel est borné à la hausse par le flux d’énergie annuel reçu par la Terre et dressé dans le bilan radiatif12 de celle-ci. Ces deux limites alliées aux seuils minimums en énergie et en matière nécessaire pour créer une unité de richesse encadreraient alors la taille maximale de l’économie mondiale soutenable sur le très long terme.
Remerciements
Je souhaiterais remercier Victor Court, Guillaume Le Borgne et Aude Pommeret pour leurs suggestions mais également les deux relecteurs anonymes de NSS pour leurs nombreuses remarques et corrections.
Références
- Arnsperger C., Bourg D., 2016. Vers une économie authentiquement circulaire. Réflexions sur les fondements d’un indicateur de circularité, Revue de l’OFCE, 145, 1, 91-125, https://doi.org/10.3917/reof.145.0091. [Google Scholar]
- Arnsperger C., Bourg D., 2017. Écologie intégrale. Pour une société permacirculaire, Paris, Presses universitaires de France. [Google Scholar]
- Ayres R.U., 2001. Resources, scarcity, growth and the environment, INSEAD Working Paper. [Google Scholar]
- Ayres R.U., 2007. On the practical limits to substitution, Ecological Economics, 61, 1, 115-128, https://doi.org/10.1016/j.ecolecon.2006.02.011. [CrossRef] [Google Scholar]
- Bihouix P., 2014. L’âge des low tech. Vers une civilisation techniquement soutenable, Paris, Seuil. [Google Scholar]
- Boutaud A., Gondran N., 2009. L’empreinte écologique, Paris, La Découverte. [Google Scholar]
- Daly H.E., 1979. Entropy, growth, and the political economy of scarcity, in Smith, V.K. (Ed.), Scarcity and growth reconsidered, Baltimore, Johns Hopkins University Press, 67-94. [Google Scholar]
- Daly H.E., 1990. Toward some operational principles of sustainable development, Ecological Economics, 2, 1, 1-6, https://doi.org/10.1016/0921-8009(90)90010-R. [CrossRef] [Google Scholar]
- Dasgupta P., Heal G., 1974. The optimal depletion of exhaustible resources, The Review of Economic Studies, 41, 5, 3-28, https://doi.org/10.2307/2296369. [CrossRef] [Google Scholar]
- Ehrlich P.R., Holdren J.P., 1971. Impact of population growth, Science, 171, 3977, 1212-1217, https://doi.org/10.1126/science.171.3977.1212. [CrossRef] [PubMed] [Google Scholar]
- Ellen MacArthur Foundation, 2019. Économie circulaire, Ellen Macarthur Foundation, www.ellenmacarthurfoundation.org/fr/economie-circulaire/ecoles-de-pensee. [Google Scholar]
- Fagnart J.-F., Germain M., 2011. Quantitative versus qualitative growth with recyclable resource, Ecological Economics, 70, 5, 929-941, https://doi.org/10.1016/j.ecolecon.2010.11.008. [CrossRef] [Google Scholar]
- Fagnart J.-F., Germain M., 2012. Les limites environnementales à la croissance en macroéconomie, Reflets et perspectives de la vie économique, 51, 4, 25-46, https://doi.org/10.3917/rpve.514.0025. [CrossRef] [Google Scholar]
- Fizaine F., Court V., 2016. Energy expenditure, economic growth, and the minimum EROI of society, Energy Policy, 95, 172-186, https://doi.org/10.1016/j.enpol.2016.04.039. [CrossRef] [Google Scholar]
- Georgescu-Roegen N.G., 1971. The entropy law and the economic process, Cambridge (Mass.), Harvard University Press. [CrossRef] [Google Scholar]
- Ghisellini P., Cialani C., Ulgiati S., 2016. A review on circular economy: the expected transition to a balanced interplay of environmental and economic systems, Journal of Cleaner Production, 114, 11-32, https://doi.org/10.1016/j.jclepro.2015.09.007. [Google Scholar]
- Grandjean A., 2011. Les conditions de la « croissance verte », Annales des Mines – Responsabilité et environnement, 61, 1, 122-127, https://doi.org/10.3917/re.061.0122. [CrossRef] [Google Scholar]
- Grosse F., Mainguy G., 2010. Is recycling “part of the solution”? The role of recycling in an expanding society and a world of finite resources, SAPIENS, 3, 1, 1-17, https://journals.openedition.org/sapiens/906#&sid=oa&domaine=inshs&doi=null. [Google Scholar]
- Grosse F., Mainguy G., 2011. Quasi-circular growth: a pragmatic approach to sustainability for non-renewable material resources, SAPIENS, 4, 2, https://journals.openedition.org/sapiens/1242#&sid=oa&domaine=inshs&doi=null. [Google Scholar]
- Jackson T., 2010. Prospérité sans croissance. La transition vers une économie durable, Bruxelles, De Boeck. [Google Scholar]
- Kirchherr J., Reike D., Hekkert M., 2017. Conceptualizing the circular economy: an analysis of 114 definitions, Resources, Conservation and Recycling, 127, 221-232, https://doi.org/10.1016/j.resconrec.2017.09.005. [Google Scholar]
- Krausmann F., Gingrich S., Eisenmenger N., Erb K.-H., Haberl H., Fisher-Kowalski M., 2009. Growth in global materials use, GDP and population during the 20th century, Ecological Economics, 68, 10, 2696-2705, https://doi.org/10.1016/j.ecolecon.2009.05.007. [CrossRef] [Google Scholar]
- Krausmann F., Wiedenhofer D., Lauk C., Haas W., Tanikawa H., Fishman T., Miatto A., Schandl H., Haberl H., 2017. Global socioeconomic material stocks rise 23-fold over the 20th century and require half of annual resource use, PNAS, 114, 8, 1880-1885, https://doi.org/10.1073/pnas.1613773114. [CrossRef] [PubMed] [Google Scholar]
- Labbé J.-F., 2016. Les limites physiques de la contribution du recyclage à l’approvisionnement en métaux, Annales des Mines – Responsabilité et environnement, 82, 2, 45-56, https://doi.org/10.3917/re1.082.0045. [CrossRef] [Google Scholar]
- Laurent E., 2011. Faut-il décourager le découplage ?, Revue de l’OFCE, 120, 1, 235-257, https://doi.org/10.3917/reof.120.0235. [Google Scholar]
- Maddison A., 2007. Contours of the world economy, 1-2030 AD. Essays in macro-economic history, Oxford, Oxford University Press. [Google Scholar]
- Maddison Project, 2013. Maddison Project Database, Version 2013, www.rug.nl/ggdc/historicaldevelopment/maddison/releases/maddison-project-database-2013?lang=en. [Google Scholar]
- McDonough W., Braungart M., 2011. Cradle to cradle. Créer et recycler à l’infini, Paris, Gallimard. [Google Scholar]
- Meadows D.H., Meadows D.L., Randers J., Behrens W.W., 1972. The limits to growth. A report for the Club of Rome’s project on the predicament of mankind, New York, Universe Books. [Google Scholar]
- MTE, 2019. L’économie circulaire, Ministère de la Transition écologique, www.ecologique-solidaire.gouv.fr/leconomie-circulaire. [Google Scholar]
- Neumayer E., 2000. Scarce or abundant? The economics of natural resource availability, Journal of Economic Surveys, 14, 3, 307-335, https://doi.org/10.1111/1467-6419.00112. [Google Scholar]
- Radetzki M., Van Duyne C., 1985. The demand for scrap and primary metal ores after a decline in secular growth, The Canadian Journal of Economics, 18, 2, 435-449, https://www.jstor.org/stable/pdf/135147.pdf. [CrossRef] [Google Scholar]
- Rockström J., Steffen W., Noone K., Persson A., Chapin F.S., III., Lambin E., Lenton T.M., Scheffer M., Folke C., Schellnhuber H.J., Nykvist B., de Wit C.A., Hughes T., van Der Leeuw S., Rodhe H., Sörlin S., Snyder V., Costanza R., Svedin U., Falkenmark M., Karlberg L., Corell R.W., Fabry V.J., Hansen J., Walker B., Liverman D., Richardson K., Crutzen P., Foley J., 2009. Planetary boundaries: exploring the safe operating space for humanity, Ecology and Society, 14, 2, 32, www.ecologyandsociety.org/vol14/iss2/art32/. [Google Scholar]
- Rotillon G., 2010. Économie des ressources naturelles, Paris, La Découverte. [Google Scholar]
- Solow R.M., 1974a. The economics of resources or the resources of economics, The American Economic Review, 64, 2, 1-14, http://www.jstor.org/stable/1816009. [Google Scholar]
- Solow R.M., 1974b. Intergenerational equity and exhaustible resources, The Review of Economic Studies, 41, 5, 29-45, https://doi.org/10.2307/2296370. [CrossRef] [Google Scholar]
- Stahel W., 2014. Reuse is the key to the circular economy, European Commission. Environment. Eco-Innovation Action Plan, https://ec.europa.eu/environment/ecoap/about-eco-innovation/experts-interviews/reuse-is-the-key-to-the-circular-economy_en. [Google Scholar]
- Steinberger J.K., Krausmann F., Eisenmenger N., 2010. Global patterns of materials use: a socioeconomic and geophysical analysis, Ecological Economics, 69, 5, 1148-1158, https://doi.org/10.1016/j.ecolecon.2009.12.009. [CrossRef] [Google Scholar]
- Stiglitz J., 1974. Growth with exhaustible natural resources: efficient and optimal growth paths, The Review of Economic Studies, 41, 5, 123-137, https://doi.org/10.2307/2296377. [CrossRef] [Google Scholar]
- Tilton J.E., 1996. Exhaustible resources and sustainable development: two different paradigms, Resources Policy, 22, 1-2, 91-97, https://doi.org/10.1016/S0301-4207(96)00024-4. [CrossRef] [Google Scholar]
- UNEP (United Nations Environment Programme), 2011. Decoupling natural resource use and environmental impacts from economic growth. A report of the working group on decoupling to the international resource panel. Fischer-Kowalski M., Swilling M., Weizsäcker E.U. von, Ren Y., Moriguchi Y., Crane W., Krausmann F., Eisenmenger N., Giljum S., Hennicke P., Romero Lankao P., Siriban Manalang A., Sewerin S., Nairobi, UNEP. [Google Scholar]
- UNEP (United Nations Environment Programme), 2016. Global material flows and resource productivity. An assessment study of the unep international resource panel. Schandl H., Fischer-Kowalski M., West J., Giljum S., Dittrich M., Eisenmenger N., Geschke A., Lieber M., Wieland H.P., Schaffartzik A., Krausmann F., Gierlinger S., Hosking K., Lenzen M., Tanikawa H., Miatto A., Fishman T., Nairobi, UNEP. [Google Scholar]
- Vivien F.-D., 1994. Économie et écologie, La Découverte. [Google Scholar]
- Weizsäcker E.U. von, Hargroves K., Smith M.H., Desha C., Stasinopoulos P., 2013. Facteur 5. Comment transformer l’économie en rendant les ressources 5 fois plus productives, Bruxelles, De Boeck. [Google Scholar]
Ce désaccord fut principalement alimenté par les possibilités de substitution des ressources naturelles par d’autres facteurs (capital, connaissances) initiées par les modèles de croissance de Dasgupta et Heal (1974), Solow (1974a ; 1974b) et Stiglitz (1974) créés dans les années 1970 en réponse au rapport de Meadows et al. (1972).
Le terme « croissance des limites » est une inversion conceptuelle des « limites à la croissance » proposées au départ par le rapport Meadows et al. (1972). Cette croissance des limites reflète bien les arguments des opposants au rapport Meadows comme Julian L. Simon. Au travers d’ouvrages comme The ultimate resource, cet économiste avance que la seule ressource importante (l’intelligence humaine/ou capital humain) permettrait de faire croître sans limites l’abondance des ressources naturelles et donc que l’homme serait en capacité de repousser sans cesse la rareté de celles-ci.
Au niveau microéconomique, l’intensité matérielle représente le rapport entre le contenu moyen de ressources/énergie nécessaire pour la production d’un produit/service et la valeur ajoutée associée à celui-ci. Une baisse de l’intensité matérielle à zéro requerrait soit que le produit soit totalement dématérialisé (consommation directe et indirecte de ressource nulle), soit que la valeur ajoutée par produit progresse sans limite à la hausse (hausse perpétuelle du prix réel du produit ou baisse perpétuelle des consommations intermédiaires du produit).
Par exemple, si le taux de recyclage de la matière en fin de vie est de 40 %, la durée de vie moyenne de la matière dans l’économie est de 50 ans, et que la croissance économique atteint 3 %, il faut que Z (vitesse de réduction de l’intensité matière) soit inférieure à la courbe noire supérieure gauche sur le graphique (−4,67 % par an).
Cela ignore toutefois d’autres conditions de soutenabilité, en particulier que le prélèvement ne soit pas supérieur au taux de régénération du stock naturel, sans quoi cela conduirait à réduire ce stock ainsi que la quantité annuelle maximale prélevable par l’économie d’un point de vue soutenable.
On peut par contre démontrer que seule une consommation de ressources constante ou décroissante (Ω ≤ 0) est compatible avec l’équation (20).
Rappelons que l’ouvrage très optimiste de Weizsäcker et al. (2013) sur l’évolution de la productivité en ressources naturelles n’évoque qu’un facteur 5.
Citation de l’article: Fizaine F. La croissance verte est-elle durable et compatible avec l’économie circulaire ? Une approche par l’identité IPAT. Nat. Sci. Soc. 29, 3, 312-325.
Liste des tableaux
Valeurs empiriques des différents paramètres du modèle sur la période 1950-2010. *Ces ressources sont potentiellement renouvelables ou peuvent être produites à partir de ressources renouvelables ; les conditions sur l’économie circulaire peuvent donc être moins restrictives que Z° et se rapprochent de Z* sur le long terme. Source : Krausmann et al. (2017), ONU, Maddison (2007) et Maddison Project (2013).
Évolution de l’intensité de différentes mesures agrégées au niveau mondial. Note : intensité matière basée sur les données de Krausmann et al. (2009), intensité énergétique basée sur les données de Fizaine et Court (2016).
Temps estimé pour atteindre un minimum en intensité matérielle selon le rapport entre la valeur initiale (VI) et le seuil minimal (a) ainsi que la vitesse de dématérialisation Z.
Liste des figures
 |
Fig. 1 Durée pour atteindre un seuil β en fonction de l’évolution de l’intensité Z. Les valeurs des paramètres Φ, Γ, C0 et β ont été fixées à 0 % ; 2 % ; 13,541 Gtep ; 91,955 Gtep. Note : Gtep signifie milliards de tonnes d’équivalent pétrole. β correspond au flux d’énergie solaire absorbé par la terre par an et C0 représente la consommation d’énergie finale actuelle humaine. |
| Dans le texte | |
 |
Fig. 2 Niveau de baisse de l’intensité matérielle nécessaire (découplage) pour concilier croissance verte illimitée et économie circulaire. Les courbes représentent le niveau nécessaire de recyclage et de variation de l’intensité matérielle pour différentes valeurs de durée de vie des produits en années. Note : Φ = 0 et Γ = 0,03. |
| Dans le texte | |
 |
Fig. 3 Vitesse de dématérialisation requise (Z) à différentes dates appliquée au cas du carton/papier. Note : λ représente le ratio entre le prélèvement maximum autorisé sur la biosphère en ressources et la consommation en ressources de l’économie initiale. Note : Φ = 0, Γ = 2 %, i = 2, α = 34 %. Dans le cas de λ = 0 (consommation primaire nulle), il faudrait que Z soit inférieur à −42 % par an. |
| Dans le texte | |
 |
Fig. 4 Évolution de la consommation d’énergie, de cuivre et de matières premières et du produit intérieur brut mondial (base 100 = 2009). Données : Maddison Project (2013), Krausmann et al. (2017), Fizaine et Court (2016). |
| Dans le texte | |
 |
Fig. 5 Bilan mondial de l’extraction de ressources naturelles par catégorie. Les ressources renouvelables (biomasse) ne représentent qu’une part minoritaire du bilan et leur poids relatif décroît. Données de l’UNEP (2016). |
| Dans le texte | |
Les statistiques affichées correspondent au cumul d'une part des vues des résumés de l'article et d'autre part des vues et téléchargements de l'article plein-texte (PDF, Full-HTML, ePub... selon les formats disponibles) sur la platefome Vision4Press.
Les statistiques sont disponibles avec un délai de 48 à 96 heures et sont mises à jour quotidiennement en semaine.
Le chargement des statistiques peut être long.





